Behandlande läkare måste ta hänsyn till osäkerheten

Det vore angenämt om tillvaron var befriad från osäkerhet – eller vore det? Intuitivt inser de flesta att mätresultat är behäftade med en osäkerhet men det kan vara svårt att klä denna i siffror. På laboratoriet får vi ofta höra att de och de värdena har blivit för höga eller för låga och det är en angelägen och nödvändig återkoppling. Samtidigt vet vi att de flesta patienter och många läkare drar en knivskarp gräns vid referensvärdets övre eller undre gräns. I det följande skall vi diskutera något av vad man kan förvänta sig i fråga om variation och avvikelser i mätresultat.

Osäkerhet i mätresultaten
Precision. Osäkerhet (se Fakta) i laboratoriernas resultat består av en del som beskriver »precisionen«, det vill säga laboratoriets förmåga att från prov till prov, från dag till dag erhålla samma resultat vid mätning av samma prov, och en del som beskriver hur nära det sanna värdet mätvärdet är, det vill säga »riktigheten«. Precision, »det tillfälliga felet«, kan förstås som »repeterbarhet«, det vill säga hur väl mätningen kan upprepas inom en mätserie, och som »reproducerbarhet«, vilket beskriver osäkerheten när mätningen upprepas vid ett annat tillfälle. Det är viktigt att känna till dessa begrepp och storheter både i rutinsjukvård och klinisk forskning.
Laboratorierna har god kontroll på precisionen genom upprepade mätningar av kända prover och precisionen skall vara tillgänglig för alla användare av laboratoriets tjänster.
Även undersökningar vilkas resultat blir »ja« eller »nej«, positivt eller negativt, är mätningar och resultaten är antingen över eller under ett gränsvärde, »cut-off«. Vid bedömningen av till exempel metoder för HIV-test eller snabbtest för streptokocker, graviditet eller urinkomponenter måste precisionen i uppskattningen av gränsvärdet inkluderas. Gränsvärdet är omgivet av en »gråzon« som motsvarar imprecisionen i mätningen vid denna koncentration. Gråzonen är ofta otillfredsställande definierad eller till och med okänd.
Riktighet. Teoretiskt kan alla mätningar bli riktiga – med en viss imprecision – eftersom man beräknar relationen mellan mätsignalen (radioaktivitet, ljusintensitet etc) och en känd koncentration, det vill säga man genomför en kalibrering av mätningen. Relationen används för att omvandla en signal till medicinska värden. Biologiska prover innehåller många störande eller potentiellt störande komponenter, så denna relation håller inte alltid.
För att bedöma riktigheten i ett svar krävs därför att den sanna koncentrationen är känd. Det är den sällan och vi tvingas därför överenskomma om ett värde på kalibratorer och kontrollmaterial på så goda grunder som möjligt, till exempel medelvärdet beräknat från många laboratoriers mätningar. Avvikelsen från ett sant eller överenskommet värde kallas »bias« och utgör det systematiska felet. Det finns internationella tabellerade riktvärden för både imprecision och »bias« för kliniskt intressanta storheter [1].
Beräkning av osäkerheten. Laboratorier är skyldiga att på begäran upplysa om metoders osäkerhet och det idealiska vore om detta angavs i svaret. Det stöter dessvärre på praktiska problem och skulle göra svarsrapporterna svårlästa. Laboratorier beräknar och anger inte heller mätosäkerheten på ett enhetligt sätt, trots – eller kanske just på grund av – att litteraturen är så omfattande. Konsensus växer dock om hur osäkerheten bör beräknas (baserad på variansanalys), inte bara tack vare grundläggande arbeten av Aronsson och medarbetare [2] utan även genom nyare litteratur [3] och globala standarder [4].

Användning av osäkerheten vid bedömning
Delta check. Läkare och patienter anses vara »siffertrogna«. Det är laboratoriets uppgift att svara för resultatens noggrannhet (riktighet och precision) men läkaren och patienten måste vid bedömningen även ta hänsyn till osäkerheten. Hur skall man då använda osäkerheten?
Laboratorievärden används framför allt i två situationer:
• diagnostiskt: Hur förhåller sig resultatet till ett givet värde?
• terapeutiskt: Har värdet ändrats under behandlingen?

Som tumregler gäller att avvikelsen från ett givet värde (utan osäkerhet), till exempel en referensvärdesgräns, skall vara omkring dubbla osäkerheten för att vara säkerställd, medan skillnaden mellan två konsekutiva mätningar (med samma osäkerhet) skall vara större än omkring tre gånger osäkerheten för att vara säkerställd med tillfredsställande sannolikhet.
Om koncentrationen av B-hemoglobin mäts med en osäkerhet av 5 procent behöver skillnaden mellan två observationer vid 120 g/l vara omkring 15 procent, det vill säga omkring 18 g/l, för att vara säkerställd.
Vid 2 procents osäkerhet blir känsligheten större, redan en skillnad av omkring 7 g/l kan anses säkerställd. Många laboratorier har långt framskridna planer på att införa så kallad delta check vilket innebär att laboratoriedatasystemet jämför det aktuella resultatet med det närmast föregående och rapporterar om skillnaden är säkerställd.
Referensintervall. Begreppet »normalvärde« är övergivet sedan länge och ersatt av »referensintervall«. En anledning till skiftet var svårigheten att definiera »normal«. En referenspopulation definieras som till exempel »män mellan 20 och 30 år« eller en definierad grupp, till exempel »gravida i sjätte månaden«. Prover samlas in under standardiserade former och aktuella storheter mäts med rutinmetoden. Definitionsvis utgör den centrala 95:e percentilen referensintervallet; om resultaten är normalfördelade sammanfaller detta med medelvärdet ±2 standardavvikelser.
Vanligen rekommenderas minst 125 individer för en beräkning av referensintervallet, vilket inte alla laboratorier mäktar med. Man har försökt harmonisera referensvärdena i hela Norden genom det så kallade NORIP-projektet [5], mycket ambitöst upplagt. Om man emellertid inte lyckas harmonisera mätprocedurerna och få överensstämmande resultat – där sviktar projektet – är dessa referensintervall inte bättre än andra som till exempel tillverkarna tillhandahåller eller som återfinns i läroböcker. Riktigheten blir avgörande för referensvärdenas generella användbarhet – och den känner vi sällan, trots externa kontrollsystem. Referensvärden kan därför aldrig bli mer än riktvärden och utfallet måste bedömas i varje enskilt fall.
Laboratorierna är formellt skyldiga att redogöra för hur de angivna referensintervallen beräknats.
Referensintervall gäller bara för individer ur referenspopulationen. Hälso- och sjukvården kan ha högre ambitioner, till exempel att minska risken för hjärt–kärlsjukdom genom vårdprogram eller terapeutiska riktlinjer. Man definierar då beslutsgränser vid vilka behandling skall övervägas. Typiska exempel kan hämtas inom lipemisfären. Referensvärden och beslutsgränser saknar definitionsmässigt osäkerhet.
En undersökningsmetods kliniska värde uttrycks ofta som dess sensitivitet och specificitet, men dessa begrepp skall inte beröras här.

Beräknade storheter
Genom att på olika sätt sammanföra resultaten av mätningar kan nya storheter skapas som har ett större diagnostiskt värde än någon av de ingående storheterna. Det är givet att osäkerheten för den beräknade storheten beror på osäkerheten i de uppmätta värdena; den sammanlagda osäkerheten blir alltid större än någon av de ingående storheternas. Osäkerheterna fortplantas enligt regler som beror på hur beräkningen utförs. Generellt kan den sammanlagda osäkerheten beräknas med hjälp av partiella derivator men i enkla fall räcker det att känna till att de absoluta eller relativa osäkerheternas kvadrater adderats i den sammanlagda variansen. Några exempel:
Anjongap. Anjongap är skillnaden mellan mängden katjoner och anjoner, vanligen beräknad från koncentrationen av natrium- , kalium- klorid- och bikarbonatjoner:

GAP=(S-Na⁺+S-K⁺)–(S-Cl^–+S-HCO_{3 ^–)}

där S-Na⁺ etc avser koncentrationen av respektive komponent i serum. Typiska värden på osäkerheterna (u) är u_S-Na: 0,4 procent, u_S-K: 2,4 procent, u_S-Cl: 0,6 procent, u_S-HCO3: 2,4 procent. Den sammanlagda osäkerheten beräknas då till 4,7 procent vilket ger ett osäkerhetsintervall vid vanliga värden (20 mmol/l) och 95 procents konfidensnivå omkring 1,9 mmol/l; annorlunda uttryckt 20 mmol/l ± 1,9 mmol/l (k=2). En minimal säkerställd skillnad mellan två resultat blir då ±3 mmol/l (95 procents konfidensintervall, ? 3 x 1,9:2).
Vi gjorde 13 konsekutiva mätningar på Li-heparinblod. Resultaten (medelvärde ± standardavvikelse) var P-Na 137 ± 0,0 mmol/l, P-K 4,35 ± 0,05 mmol/l, P-Cl 109 ± 0,6 mmol/l och P-HCO³ 25,9 ± 0,3 mmol/l.
Anjongapet beräknades till 15,5 ± 0,8 mmol/l det vill säga variationskoeficienten (CV%): 5,5. Den funna sammanlagda osäkerheten blir av samma storleksordning som den teoretiska. Den minsta säkerställda skillnaden mellan två resultat uppgår till omkring 2,5 mmol/l (0,8×3).
LDL-kolesterol. Beräkning av LDL-kolesterol och därmed förknippade problem och osäkerheter beskrevs nyligen utförligt i Läkartidningen [6]. Den huvudsakliga osäkerhetskällan visades vara kolesterol och man kan uppskatta standardosäkerheten till omkring 6 procent, det vill säga det fordras en skillnad av omkring 18 procent mellan två mätvärden (6,5 – 5,5 = 1,0; dvs 18 procent).
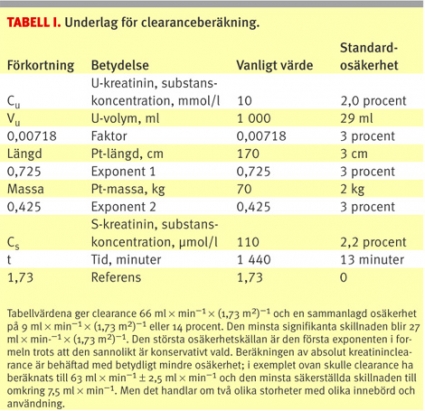
Kreatininclearance. Beräkningen av kreatininclearance med korrektion för kroppsytan utförs enligt du Bois´ algoritm (nomogram finns i Fass). Mätvärdenas osäkerhet är hämtade från Karolinska universitetslaboratoriet medan osäkerheten för volym, tid, längd och massa och för faktorn och exponenterna skattats enligt gängse regler (se Tabell I). Resultatet kallas även »relative creatinine clearance« till skillnad från absolut kreatininclearance där ingen korrektion för kroppsytan utförs:

(Se figur A)

Övriga beräknade storheter. Ett annat exempel på en storhet som beräknas är »albuminkorrigerat kalcium«. I Sverige har man identifierat minst 17 olika algoritmer vilka bygger på att totala kalciumkoncentrationen korrigeras med en bråkdel (0,01–0,05) av skillnaden mellan en uppmätt albuminkoncentration och en antagen »standardkoncentration« av albumin. I Sverige varierar denna mellan omkring 40 och 42 g/l, internationellt mellan 36 och 52 g/l. »Korrektionen« blir således större ju mer albuminvärdet avviker från standardvärdet, vilket stämmer med teorin, men blir beroende av bråkdelen och vilken standardkoncentration som valts. Ett är säkert, med nuvarande godtycklighet blir varken resultat eller erfarenheter överförbara eller jämförbara mellan olika sjukvårdsinrättningar.
Beräkningen av glomerular filtration rate (GFR) från S-kreatinin (MDRD eller Cockroft–Gaults formel) eller S-cystatin C är andra exempel. Algoritmerna innehåller konstanter, faktorer och exponenter som beräknats genom matematisk anpassning till GFR, beräknat genom iohexolinjektion som i sin tur anpassats till inulin- eller ⁵¹Cr-EDTA-clearance. Osäkerheten i faktorerna är i regel okänd men även en måttlig osäkerhet i till exempel en exponent kan leda till betydande osäkerhet i resultaten. Man »lurar« klinikerna genom att förvandla ett mätvärde till något som storleksmässigt liknar en given storhet men som genom denna manipulation har en större osäkerhet.
Man kan identifiera dels beräknade storheter där bara de mätta storheterna ingår, till exempel anjongap, Apo B/Apo A1- kvoten och absolut kreatininclearance, dels storheter som skapas med beräknade proportionalitetsfaktorer och så vidare, genom matematisk anpassning (t ex MDRD). De förra kan motiveras med att man då väger in mer än ett resultat och det kan skärpa den diagnostiska förmågan, medan det är svårt att motivera den senare typen av storheter som avser att »simulera« vanligtvis mätta storheter. Man skapar nya storheter baserade på mätningar som användaren vanligen varken har förståelse för, inflytande över eller med säkerhet kan upprepa.

Osäkerheten i praktiken
Kunskap om mätningars osäkerhet har stor betydelse när resultaten av undersökningen ligger nära en besluts- eller referensvärdesgräns. Om avståndet till beslutsgränsen är stort spelar osäkerheten mindre roll. Det är i närheten av gränsvärden som falska positiva och negativa svar ger sig till känna.
Ur Figur1 kan man lätt uppskatta viken minsta skillnad som behövs för att två mätvärden säkert skall vara åtskilda.

Sammanfattning
I denna framställning har vi inte alls berört olika osäkerhetskällor. För många storheter är den preanalytiska variationen avgörande. Har patienten fastat som föreskrivet? Har provtagningen skett med eller utan stas? Har provet transporterats och förbehandlats (till exempel centrifugerats) korrekt? Det är en vanlig uppfattning att sådana osäkerhetskällor inte kan behandlas statistiskt utan att man endast kan minimera dem genom utbildning och engagemang från patienter och sjukvårdspersonal.
Kännedom om mätosäkerheten i resultat från numeriska mätningar ger en fingervisning om hur stora skillnader mellan konsekutiva resultat som fordras för en säkerställd skillnad. Osäkerheten kan också användas för att bedöma osäkerheten i beräknade storheter. Det bör understrykas att även osäkerhetsberäkningar är förknippade med osäkerhet beroende på ingående data. Det kan därför vara vanskligt att dra alltför långtgående slutsatser från dessa osäkerhetsberäkningar.
*
Potentiella bindningar eller jävsförhållanden: Inga uppgivna.

Figur A