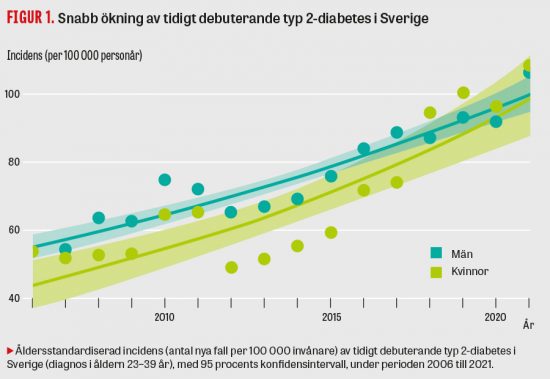
Sammanfattat
Med Bayes’ sats kan man, med känd sensitivitet, specificitet och sjukdomsprevalens, beräkna sannolikheten för att ett positivt testresultat är sant positivt.
Eftersom prevalensen ofta är låg, kommer även ett bra test att medföra att ett positivt resultat mest sannolikt är falskt positivt. Man bör alltså inte förlita sig på ett enkelt test.
Det är bra att kunna Bayes’ sats, men viktigast är att ha en känsla för ovanstående resonemang.
För att inte skrämma iväg alltför många läsare med sannolikhetslära vill jag börja med ett exempel som skulle kunna förekomma i den kliniska vardagen. Antag att vi har ett test för t ex HIV med 99 procents sensitivitet (om man undersöker HIV-bärare med detta test kommer man att i medel få positivt utfall i 99 fall av 100) och 99 procents specificitet (om man undersöker icke-HIV-bärare med detta test kommer man att i medel få negativt utfall i 99 fall av 100). I klinisk praxis är detta ett mycket bra test. Ska vi då testa alla i Grönköping med detta test? Låt oss anta att prevalensen är 0,5 procent. Vi har alltså följande situation:
• sensitivitet 99 procent
• specificitet 99 procent
• prevalens 0,5 procent.
Vad är då sannolikheten för HIV-bärarskap om vi har positivt test?
A) 90 procent
B) 50 procent
C) 33 procent.
Intuitivt skulle man kunna tycka att sannolikheten borde bli ganska hög, eftersom vårt utmärkta test utföll positivt. Skulle det vara 33 procent är det mer sannolikt att personen inte är HIV-bärare än att personen vore det! I anglosaxisk litteratur kallas ibland prevalensen för pre-test probability, medan sannolikheten för HIV om vi har ett positivt test kallas för post-test probability. Vi återkommer strax till detta illustrativa exempel.
Så räknar man fram Bayes’ sats
Låt oss som brukligt beteckna sannolikheten för händelsen HIV-bärarskap med P(HIV). Antingen är man HIV-bärare eller så är man det inte, alltså P(HIV) + P(ej HIV) = 1, varur följer P(HIV) = 1 – P(ej HIV).
Vi behöver införa begreppet betingad sannolikhet. Om man undersöker HIV-bärare med ett test kan man få positivt utfall (+) eller negativt utfall (–). Givet att man är HIV-bärare så betecknas sannolikheten för positivt utfall P(+|HIV). Detta är inget annat än vårt tests sensitivitet. Hur definieras då denna sannolikhet? Antag att det i Grönköping finns 20 000 personer och att alla dessa testats med vårt test och att man vet vilka som är HIV-bärare:
På grund av artikelns innehåll och fortsatta utformning med många matematiska formler och uträkningar (som inte kan visas här) hänvisar vi till nedladdningsbar pdf. red