Företrädare för Registercentrum Syd har i en tidigare artikel i Läkartidningen [1] påpekat att EQ-5D-index, ett av de vanligaste måtten för kvalitetsuppföljning i Sverige, är ett svårtolkat utvärderingsinstrument. Debattartikeln har lett till att antal diskussioner och försök att kringgå problemen genom ett antal finurliga analysmetoder. Svårigheterna med EQ-5D är emellertid inte enbart beräkningstekniska utan framför allt tolkningsmässiga.
EQ-5D-index mäter livskvalitet med ett tal mellan –0,594 och 1 och baseras på en sammanvägning av svaren på fem olika frågor. Viktningen av de olika svarsalternativen ger indexet en uni-, bi- eller trimodal fördelning beroende på egenskaperna hos de studerade individerna. Individer med full hälsa har indexvärdet 1,0. De flesta patientpopulationer uppvisar därför i en tvärsnittsundersökning bi- eller trimodala fördelningar. Det kan lätt visas att förändringen mellan två sådana indexmätningar i många fall blir multimodal.
För hypotesprövningar av, och beräkningar av konfidensintervall för, EQ-5D-index medelvärde är modaliteten och frånvaron av normalfördelning inget stort problem, åtminstone inte i stora material. Den för statistisk inferens grundläggande centrala gränsvärdessatsen säger nämligen att fördelningen av stickprovsmedelvärden blir alltmer normalfördelad med tilltagande stickprovsstorlek, oavsett ur vilken fördelning stickproven dras. En enkel simulering visar att en stickprovsstorlek på 25–30 observationer räcker för att beräkningarna ska vara tillförlitliga, under förutsättning att icke-parametriska test undviks.
Det finns nämligen ett allmänt missförstånd att icke-parametriska test är ett slags reservtest, som alltid kan ersätta Students t-test, ANOVA etc vid test av variabler som inte är normalfördelade. Det stämmer inte eftersom även icke-parametriska test baseras på antaganden. I vissa fall kan användandet av ett icke-parametriskt test vara ett allvarligt misstag. Mann–Whitney U-test (MW) förutsätter t ex att testade variabler har samma form [2]. Detta är ett orealistiskt antagande när det finns golv- och takeffekter, vilka är vanliga vid patientrapporterade utfall. Det är välkänt [2, 3] att man under sådana omständigheter kan få kraftigt missvisande resultat. Här är ett exempel.
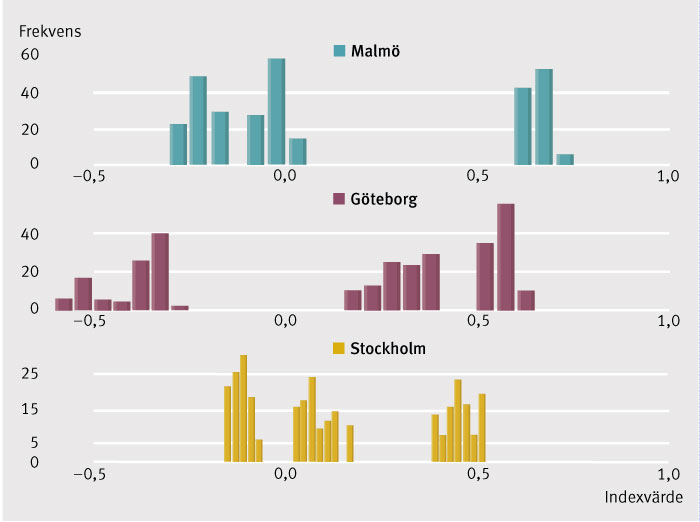
Exempel 1. Malmö är bättre än Malmö, och samma sak gäller för Göteborg och Stockholm. Figur 1 visar fiktiva EQ-5D-indexdata mätta för tre kliniker med 300 patienter vardera: Malmö, Göteborg och Stockholm. Med MW kan man visa att sannolikheten för att en patient från Malmö har bättre EQ-5D-indexvärde än en patient från Göteborg är 56 procent (p=0,02). Sannolikheten att Göteborg är bättre än Stockholm är också 56 procent (p=0,02). Det uppseendeväckande är emellertid att sannolikheten för att en patient från Stockholm har bättre EQ-5D-indexvärde än en patient från Malmö också är 56 procent (p=0,02). Den absurda slutsatsen blir alltså att alla sjukhusen är bättre än sig själva (p=0,02) samtidigt som de också är sämre än sig själva (p=0,02). Den intresserade läsaren kan ladda ned dessa data från ‹www.rcsyd.se› och själv göra om testen.
Att tolka medelvärdet (och medianen) är ett större problem än att testa det. I en normalfördelning representerar medelvärdet hela populationen. Vid oförändrad varians representerar en förbättring av medelvärdet en förbättring för hela populationen.
För EQ-5D-index är situationen annorlunda. En normalfördelning har två parameterar, medelvärde och varians. En EQ-5D-indexfördelning har fler, och en bi- eller multimodal EQ-5D-indexfördelning har betydligt fler. Att bara mäta två av dem är, som visades i den förra artikeln [1], ett misstag. Flera olika fördelningar kan nämligen dölja sig bakom samma medelvärde och varians. De praktiska konsekvenserna av detta är flera. Dels kan stora förändringar i fördelningen av patienters hälsa förbli oupptäckta, dels kan en förbättring av EQ-5D-index medelvärde uppnås på bekostnad av vissa patienters hälsa. Här är ett sådant exempel.
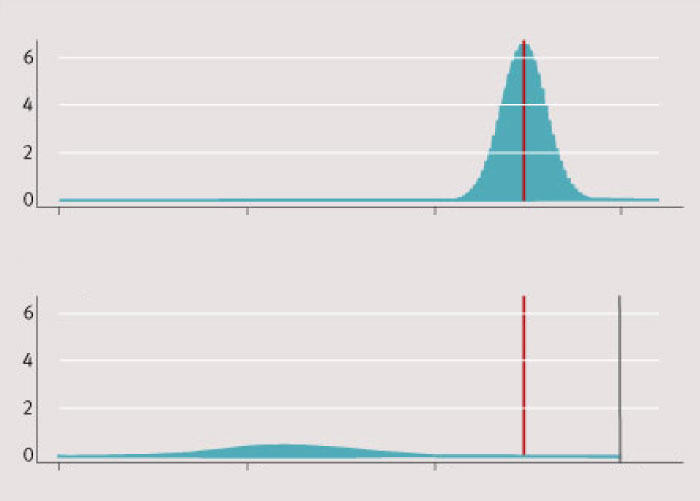
Exempel 2. Orättvis förbättring. Figur 2 visar en patientpopulation före och efter en hypotetisk behandling, säg ett nytt effektivt läkemedel med svåra biverkningar för en del av patienterna. Före behandlingen har patienterna måttliga besvär (minst en tvåa på någon av de fem EQ-5D-frågorna, men ingen trea). Efter behandlingen är 80 procent av patienterna helt friska, medan 20 procent har svåra besvär (minst en trea på någon av frågorna). Behandlingen har således visserligen förbättrat EQ-5D-index medelvärde från 0,74 till 0,83, men på bekostnad av att 20 procent av patienterna blivit sjukare.
Till skillnad från ett förbättrat normalfördelningsmedelvärde representerar alltså ett förbättrat EQ-5D-indexmedelvärde inte nödvändigtvis en förbättring för hela populationen. Om ökad jämlikhet i vården i sig utgör en förbättring kan man helt enkelt inte använda EQ-5D-index i sin utvärdering. Skulle man däremot vara intresserad av att mäta enbart den totala ohälsan, och inte dess fördelning, kan EQ-5D-index medelvärde användas på gruppnivå, t ex för att värdera kostnaden för en viss behandling i en viss grupp av patienter. Även här kan det finnas analysproblem [4], men medelvärdet kan i alla fall tolkas i termer av standardiserad total ohälsa. Jämförelser mellan olika behandlingar kan också vara meningsfulla och i överensstämmelse med undersökningens målsättning.
Att använda EQ-5D-index som utvärderingsintrument innebär däremot uppenbara risker för ökade ojämlikheter i vården, även när p-värden och konfidensintervall är korrekta.